Artificial Intelligence and the COVID-19 Black Swan

For most people, the global pandemic that is COVID-19 infecting a significant part of the global population came as a total surprise. This virus sure looked like what most people recognized as Influenza or the flu: a seasonal virus that causes a respiratory disease that causes mainly minor symptoms like fever, cough, and headaches. All the information coming from China, the known source of the disease, in early 2020, showed that if the flu was like a domestic cat, COVID-19 looked more like a hungry tiger: capable of causing much worse symptoms, and with a case mortality rate that is a factor higher than the seasonal flu. Nevertheless, both civilians and politicians were slow to respond, and to the detriment of many people's health and lives, slow to react.

Why was the world so slow to react? Why didn't we take precautions early to prevent the spread of the disease? To explain our response to COVID-19, look no further than Aristotle. In Rhetoric, Aristotle wrote:

The probable is that, for the most part, happens.

This simple logic seems to be the basis for much of human thinking - it is unlikely that this flu is particularly deadly because, for the most part, it hasn't been. This problem is called the normalcy bias - the tendency to believe that things will function in the future the same way that they have happened in the past. Solving this normalcy bias, however, is harder said than done.

A brief history of calculating probabilities

Mathematicians have fought for centuries to properly define how to calculate the probability of things happening. Building on Aristotle's logic, a whole slew of esteemed mathematicians have built ideas and techniques with what looks like the overt goal of torturing schoolchildren and students: Venn and his diagrams, Poisson and his distribution probabilities, Boole and his algebra, etc. For the most part though, these mathematicians thought of the probability of something happening as the relative frequency of this event in many random trials. In the real world, the approach of these mathematicians (called frequentists) has suffered from a pretty strict requirement: namely that in order to find a probability, one needs to be able to execute a potentially infinite sequence of randomized experiments.

In the early 1800's, an English mathematician called Thomas Bayes attempted to solve this specific problem by introducing a radically new concept: Bayes thought of calculating probabilities as a process of updating beliefs in light of new evidence. For any prediction you'd want to make, you'd start with your best possible estimate based on your knowledge and beliefs (known as your prior), and with each observation, you'd re-evaluate your belief. A common question Bayesians use to mock their (clearly inferior, they'll say) Frequentist colleagues, is this: "what is the chance that a pregnant woman who has had 5 boys will give birth to another boy?" A Bayesian's prior belief would be that women have about an equal chance to give birth to boys and girls, so would estimate the chance at 1 out of 2. A (badly trained) Frequentist would more likely give it a 100% chance.

Statistics and Black Swans

You might argue that there's no point in calculating the probability of events like COVID-19, because they are, by nature, rare and unpredictable. Nassim Taleb, who coined the Black Swan Theory, argues that such "Black Swan Events" have three central characteristics: 1. they have a disproportionate effect; 2. their probability cannot be computed; 3. people tend to have a post-hoc rationalization of the event.

Taleb argues that the best way to deal with Black Swan events does not even attempt to predict them, but to make a "contrarian bet": attribute a small (but not insignificant) part of your resources to prepare (or, as he did in his past as a trader, benefit) from a Black Swan event, and attribute the rest of your resources to low-risk venues.

Taleb and Machine Learning

Taleb's arguments have often been parroted in the machine learning community: because machine learning algorithms learn by example, you cannot teach them things for which you don't actually have any examples. Past Black Swans are likely to be irrelevant in the current context, and even if the data were available, machine learning algorithms tend to have difficulty predicting rare events, simply because they are rare. The traditional approach then has to largely accept that Black Swans might happen, but not attempt to predict them at all.

While Taleb's strategy for dealing with the outcome of a Black Swan might seem sensible, we believe that most, if not all, Black Swan events can actually be detected early, given the right data and the right algorithms.

Bayes and Anomaly Prediction

The idea of Bayesian logic can be used as a framework to better understand how to detect anomalies. If you remember, Bayes' central theorem was to update your beliefs in light of new evidence. The same principles of Bayesian inference can be used to detect anomalies.

The idea is simple: firstly, collect as much data of a period that you consider as "normal" for a particular process. For example, if the process for which you are trying to detect a Black Swan is the seasonal flu, the data you can collect could be the daily new infections, the hospitalization rate, the number of patients who are in ICU, the quality of healthcare, and any other variable that might describe the environment you're looking to describe.

Secondly, train a machine learning algorithm on your data that is auto-descriptive, such as Principal Component Analysis or auto-encoders. These algorithms take your data as input and attempt to output that exact same data. The better the algorithms outputs that same data, the lower the model error is. Typically, these algorithms are used to perform something called "dimensionality reduction" - namely attempting to encode a very complex relationship in something simple and easier to understand, often for the purpose of data visualization or analytics. In our case, this is not the goal - we only want to have a model that has a mathematical representation of "normalcy".

Our third and final step is to start using this model to then use this mathematical representation of "normalcy" to predict new data points, and measure to which extent a model is making errors. We've shown an example of this approach below.

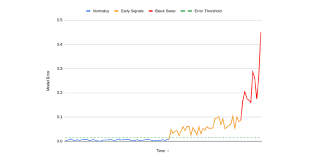
In this example, we can see three periods - in the Normalcy period, the model is not generating any significant error, meaning that it is correctly describing a period that is considered normal. In the Early Signals period, we notice that the model's errors are starting to increase quite significantly, indicating that firstly, our model doesn't recognize the properties our data is taking anymore, and secondly, that our prior belief (the situation is "normal") is likely to be false. Indeed - our final period indicates that a Black Swan event is happening: our model is totally lost and starts generating very large errors. Fundamentally, our model's error is describing whether the improbable (e.g. a Pandemic Flu) is happening.

This innovative approach opens the door in many fields - whether it's Epidemiology, Finance, Healthcare, and many more areas.

Are you currently wondering how to use AI to your benefit during and after the Covid-19 crisis? Just pick a 20 min slot for an introductory chat, or simply leave us a message and our team will answer your questions!